復合梁正應力分布規律實驗
一、實驗目的
1. 用電測法測定疊梁,復合梁在彎曲受力狀態下,沿其橫截面高度的正應變(正應力)分布規律。
2. 推導疊梁,復合梁的正應力計算公式。
二、實驗儀器和設備
1. 純彎曲梁實驗裝置(純彎曲梁復合梁)。
2. 靜態數字電阻應變儀。
三、實驗原理及步驟
1. 實驗原理
復合梁的材料為鋁梁和鋼梁,上層是鋁梁,其彈性模量分別為E=70GN/m2和E=210GN/m2。復合梁上總過貼上了12各應變片,每個梁各6個。
1. 幾何、物理和靜力學關系
以材料尺寸相同的兩層矩形截面復合梁在純彎 曲情況下為計算模型,在其縱向對稱面內,承受彎矩 M的作用。上梁的彈性模量為E1,橫截面面積為A1,下梁的彈性模量為E2,橫截面面積為A2,且A1=A2,單梁的梁寬和梁高分別為b和h,在其縱向對稱面內,承受彎矩M的作用。兩種不同的材料由膠粘合制成。下面建立橫截面上的彎曲正應力公式,平面假設與單向假設均成立。
設中性層的曲率半徑為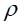 ,并沿截面縱向對稱軸與中性軸分別建立坐標軸y與z,中性層離交界面的距離為e。
,并沿截面縱向對稱軸與中性軸分別建立坐標軸y與z,中性層離交界面的距離為e。
(1)變形幾何關系。根據平面假設可知,橫截面上y處的縱向正應變為:
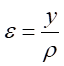 (6-1)
(6-1)
(2)物理關系。依胡克定律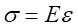 ,而
,而 由式(1)帶入,可以得出不同材料區的彎曲正應力分別為:
由式(1)帶入,可以得出不同材料區的彎曲正應力分別為:
 ,
,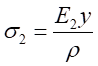 (6-2)
(6-2)
(3)靜力學平衡關系。根據受力分析,由靜力學平衡關系,考慮橫截面上內力的平衡,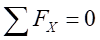 ,可以得出:
,可以得出:
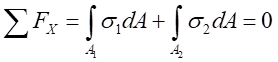 (6-3)
(6-3)
由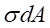 組成的內力系,在橫截面上形成一個內力偶矩M,即為橫截面上的彎矩M,即:
組成的內力系,在橫截面上形成一個內力偶矩M,即為橫截面上的彎矩M,即:
 (6-4)
(6-4)
2. 確定中性層位置
將式(2)代入式(3)中,得
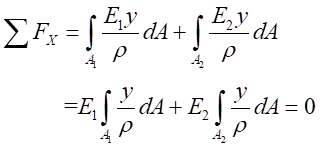
令
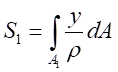
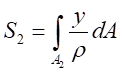
則
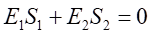 (6-5)
(6-5)
則
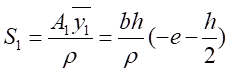
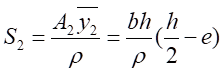
并且,令

將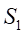 和
和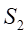 帶入式(5)得:
帶入式(5)得:
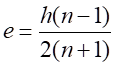 (6-6)
(6-6)
3. 推導彎曲正應力計算公式
將式(2)代入式(4),得:
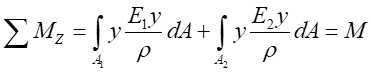
令
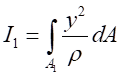 ,
,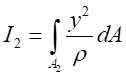
其中 、
、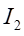 分別為截面
分別為截面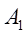 、
、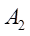 對中性軸的慣性矩。由于各梁曲率相同,經變化得:
對中性軸的慣性矩。由于各梁曲率相同,經變化得:
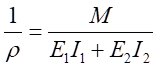 (6-7)
(6-7)
再將式(7)代入式(2),得:
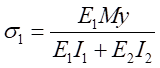 ,
,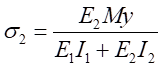 (6-8)
(6-8)
式中 、
、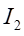 分別為
分別為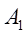 、
、 對共同中性軸Z的慣性矩。
對共同中性軸Z的慣性矩。
由單向應力狀態的虎克定律公式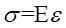 ,可求出應力實驗值。應力實驗值與應力理論值進行比較,以驗證復合梁的正應力計算公式。
,可求出應力實驗值。應力實驗值與應力理論值進行比較,以驗證復合梁的正應力計算公式。
2. 實驗步驟
1. 首先確定單梁的物理參數,得到h=20mm,b=20mm,c=150mm。
2. 啟動實驗裝置,將各應變片分別接到各個AB通道之間,同時把公共補償片接到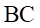 上,并且把C通道與短接片短接。
上,并且把C通道與短接片短接。
3. 進行實驗:
a.取初載荷0.5kN,每次逐級加1.0kN,直至4.5kN,總共分4次加載。
b.接完線路以及加初載荷之前都要重復置零。
c.每次加載完畢都要記錄下數據。
四、實驗數據
表6-1 Ⅰ梁應變數據表

表6-2 Ⅱ梁應變數據表
 五、數據處理
五、數據處理
1. 根據實驗數據計算各點的平均應變,求出各點的實驗應力值,并計算出各點的理論應力值;計算實驗應力值與理論應力值的相對誤差。
答:根據上面實驗數據,結合材料力學相關知識計算如下:
(1)由實驗數據可知,各應變片處的平均應變值為:
Ⅰ梁上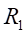 處的平均應變為:
處的平均應變為:
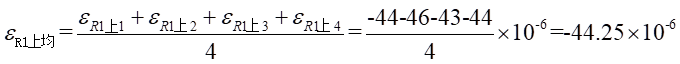
Ⅰ梁上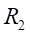 處的平均應變為:
處的平均應變為:

Ⅰ梁上 處的平均應變為:
處的平均應變為:
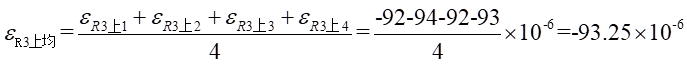
Ⅰ梁上 處的平均應變為:
處的平均應變為:
Ⅰ梁上 處的平均應變為:
處的平均應變為:
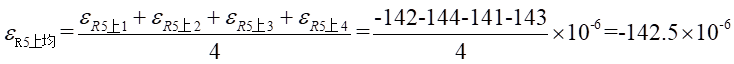
Ⅰ梁上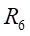 處的平均應變為:
處的平均應變為:
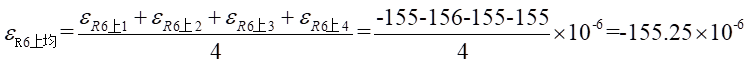
Ⅱ梁上處的平均應變為:
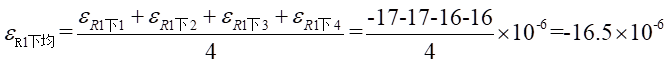
Ⅱ梁上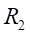 處的平均應變為:
處的平均應變為:
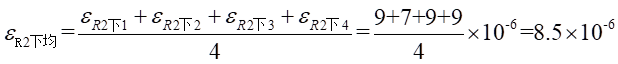
Ⅱ梁上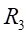 處的平均應變為:
處的平均應變為:

Ⅱ梁上 處的平均應變為:
處的平均應變為:
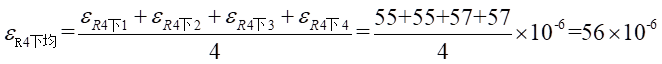
Ⅱ梁上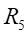 處的平均應變為:
處的平均應變為:
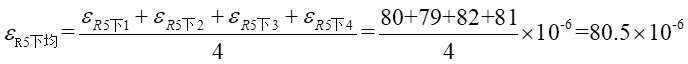
Ⅱ梁上 處的平均應變為:
處的平均應變為:

(2)各應變片處的實驗應力值為:
Ⅰ梁上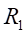 處的應力值為:
處的應力值為:

Ⅰ梁上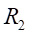 處的應力值為:
處的應力值為:
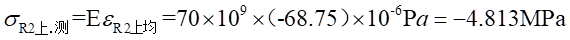
Ⅰ梁上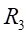 處的應力值為:
處的應力值為:
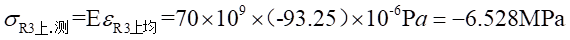
Ⅰ梁上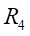 處的應力值為:
處的應力值為:
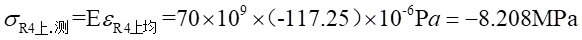
Ⅰ梁上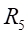 處的應力值為:
處的應力值為:
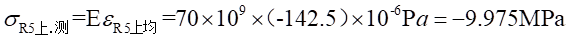
Ⅰ梁上 處的應力值為:
處的應力值為:

Ⅱ梁上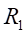 處的應力值為:
處的應力值為:
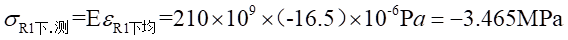
Ⅱ梁上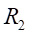 處的應力值為:
處的應力值為:
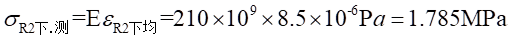
Ⅱ梁上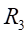 處的應力值為:
處的應力值為:
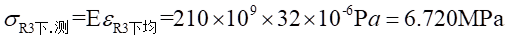
Ⅱ梁上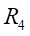 處的應力值為:
處的應力值為:

Ⅱ梁上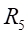 處的應力值為:
處的應力值為:
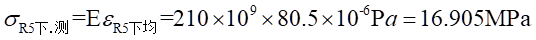
Ⅱ梁上 處的應力值為:
處的應力值為:
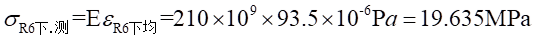
(3)理論計算試件上個應變片處的理論應力值
加載的力的大小為F=1000N。復合梁的單梁截面厚度b=20mm,高度h=20mm,截面作用點到梁支點的距離為c=150mm。設n=E2/E1=210/70=3,中性軸位置的偏移量為:
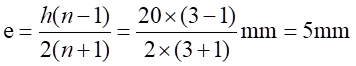
因此,可得到復合梁Ⅰ和復合梁Ⅱ正應力計算公式分別為
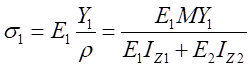
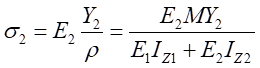
其中
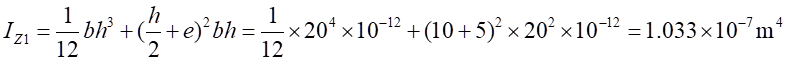
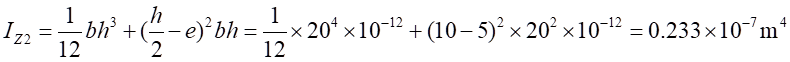
根據材料力學知識分析如下:
Ⅰ梁上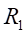 處計算應力值為:
處計算應力值為:
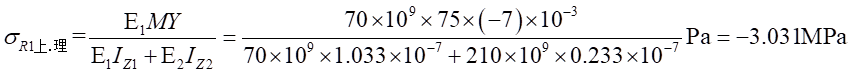
Ⅰ梁上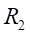 處計算應力值為:
處計算應力值為:
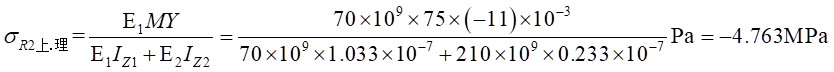
Ⅰ梁上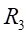 處計算應力值為:
處計算應力值為:

Ⅰ梁上 處計算應力值為:
處計算應力值為:

Ⅰ梁上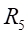 處計算應力值為:
處計算應力值為:
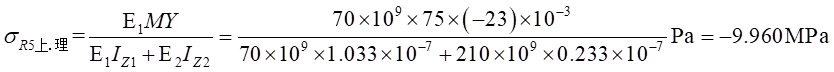
Ⅰ梁上 處計算應力值為:
處計算應力值為:
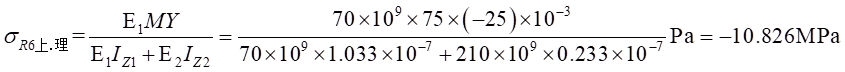
Ⅱ梁上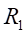 處計算應力值為:
處計算應力值為:
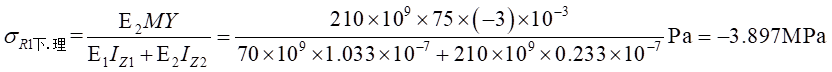
Ⅱ梁上 處計算應力值為:
處計算應力值為:
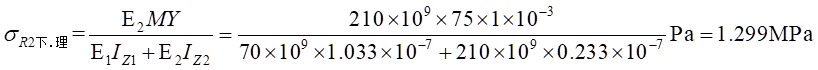
Ⅱ梁上 處計算應力值為:
處計算應力值為:

Ⅱ梁上 處計算應力值為:
處計算應力值為:
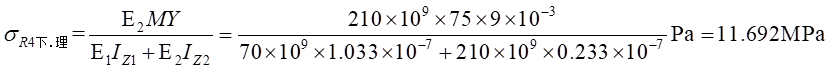
Ⅱ梁上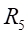 處計算應力值為:
處計算應力值為:

Ⅱ梁上 處計算應力值為:
處計算應力值為:
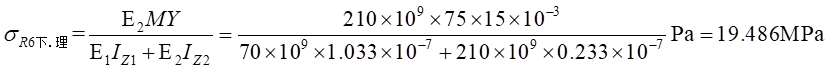
(4)計算實驗應力值與理論應力值的相對誤差
Ⅰ梁上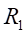 處應力值的相對誤差為:
處應力值的相對誤差為:
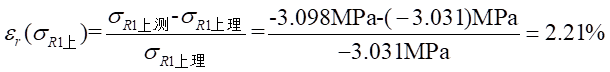
Ⅰ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:
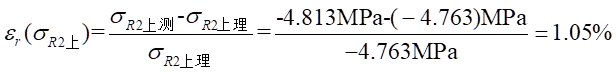
Ⅰ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:
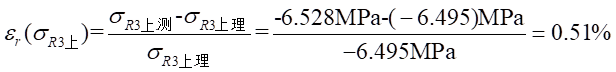
Ⅰ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:

Ⅰ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:
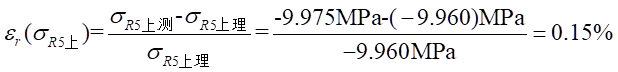
Ⅰ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:
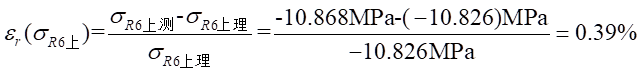
Ⅱ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:
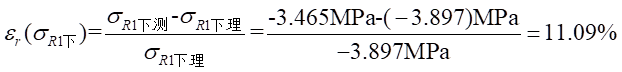
Ⅱ梁上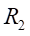 處應力值的相對誤差為:
處應力值的相對誤差為:
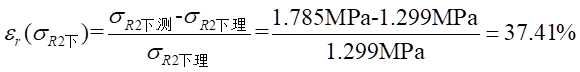
Ⅱ梁上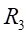 處應力值的相對誤差為:
處應力值的相對誤差為:
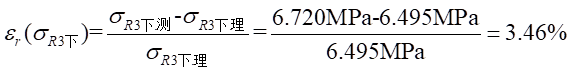
Ⅱ梁上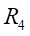 處應力值的相對誤差為:
處應力值的相對誤差為:
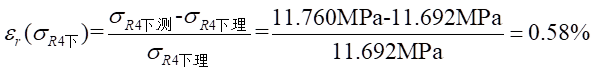
Ⅱ梁上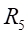 處應力值的相對誤差為:
處應力值的相對誤差為:
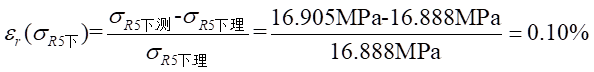
Ⅱ梁上 處應力值的相對誤差為:
處應力值的相對誤差為:

2. 上述的各點應力的實驗值與應力的理論值,將兩者進行比較。可以得出:實驗值與理論值的結果十分接近,說明復合梁的正應力計算公式成立。
六、實驗結果
根據前面計算可以看出,實驗計算的結果和理論計算的結果基本吻合。現列表如下:
表6-2 結果對比表
一、實驗目的
1. 用電測法測定疊梁,復合梁在彎曲受力狀態下,沿其橫截面高度的正應變(正應力)分布規律。
2. 推導疊梁,復合梁的正應力計算公式。
二、實驗儀器和設備
1. 純彎曲梁實驗裝置(純彎曲梁復合梁)。
2. 靜態數字電阻應變儀。
三、實驗原理及步驟
1. 實驗原理
復合梁的材料為鋁梁和鋼梁,上層是鋁梁,其彈性模量分別為E=70GN/m2和E=210GN/m2。復合梁上總過貼上了12各應變片,每個梁各6個。
1. 幾何、物理和靜力學關系
以材料尺寸相同的兩層矩形截面復合梁在純彎 曲情況下為計算模型,在其縱向對稱面內,承受彎矩 M的作用。上梁的彈性模量為E1,橫截面面積為A1,下梁的彈性模量為E2,橫截面面積為A2,且A1=A2,單梁的梁寬和梁高分別為b和h,在其縱向對稱面內,承受彎矩M的作用。兩種不同的材料由膠粘合制成。下面建立橫截面上的彎曲正應力公式,平面假設與單向假設均成立。
設中性層的曲率半徑為
(1)變形幾何關系。根據平面假設可知,橫截面上y處的縱向正應變為:
(2)物理關系。依胡克定律
(3)靜力學平衡關系。根據受力分析,由靜力學平衡關系,考慮橫截面上內力的平衡,
由
2. 確定中性層位置
將式(2)代入式(3)中,得
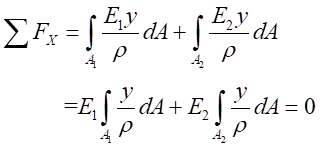
令
則
則
并且,令
將
3. 推導彎曲正應力計算公式
將式(2)代入式(4),得:
令
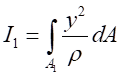 ,
,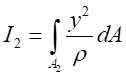
其中
再將式(7)代入式(2),得:
式中
由單向應力狀態的虎克定律公式
2. 實驗步驟
1. 首先確定單梁的物理參數,得到h=20mm,b=20mm,c=150mm。
2. 啟動實驗裝置,將各應變片分別接到各個AB通道之間,同時把公共補償片接到
3. 進行實驗:
a.取初載荷0.5kN,每次逐級加1.0kN,直至4.5kN,總共分4次加載。
b.接完線路以及加初載荷之前都要重復置零。
c.每次加載完畢都要記錄下數據。
四、實驗數據
表6-1 Ⅰ梁應變數據表

表6-2 Ⅱ梁應變數據表
 五、數據處理
五、數據處理1. 根據實驗數據計算各點的平均應變,求出各點的實驗應力值,并計算出各點的理論應力值;計算實驗應力值與理論應力值的相對誤差。
答:根據上面實驗數據,結合材料力學相關知識計算如下:
(1)由實驗數據可知,各應變片處的平均應變值為:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上處的平均應變為:
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(2)各應變片處的實驗應力值為:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(3)理論計算試件上個應變片處的理論應力值
加載的力的大小為F=1000N。復合梁的單梁截面厚度b=20mm,高度h=20mm,截面作用點到梁支點的距離為c=150mm。設n=E2/E1=210/70=3,中性軸位置的偏移量為:
因此,可得到復合梁Ⅰ和復合梁Ⅱ正應力計算公式分別為
其中
根據材料力學知識分析如下:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(4)計算實驗應力值與理論應力值的相對誤差
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
2. 上述的各點應力的實驗值與應力的理論值,將兩者進行比較。可以得出:實驗值與理論值的結果十分接近,說明復合梁的正應力計算公式成立。
六、實驗結果
根據前面計算可以看出,實驗計算的結果和理論計算的結果基本吻合。現列表如下:
表6-2 結果對比表
| 梁 | Ⅰ梁 | Ⅱ梁 | ||||||||||
| 應變片 |
|
|
|
|
|
|
|
|
|
|
|
|
| 相對中性軸的坐標y/mm | -7 | -11 | -15 | -19 | -23 | -25 | -3 | 1 | 5 | 9 | 13 | 15 |
| 實驗應力值/MPa | -3.1 | -4.8 | -6.5 | -8.2 | -10.0 | -10.9 | -3.5 | 1.8 | 6.7 | 11.8 | 16.9 | 19.6 |
| 理論應力值/MPa | -3.0 | -4.8 | -6.5 | -8.2 | -10.0 | -10.8 | -3.9 | 1.3 | 6.5 | 11.7 | 16.9 | 19.5 |
| 相對誤差/% | 2.2 | 1.1 | 0.5 | 0.2 | 0.2 | 0.4 | 11.1 | 37.4 | 3.5 | 0.6 | 0.1 | 0.8 |
從表中可以看出,理論計算和實驗結果基本吻合,相對誤差不大。實驗從某種方面上證實了理論知識。數據可用。
七、思考題
1. 復合梁中性層為何偏移?
答:因為兩種材料的抗彎能力以及抗拉能力不同,導致在同等應力條件下,兩個截面對稱位置發生的應變不同。抗彎能力以及抗拉能力強的材料發生的變形小于另一種材料,因此中性層就向下偏移了。
2. 如何理解復合梁實驗中出現兩個中性層?
復合梁雖然中間是由物理或化學方法進行了連接,但是其實際上不是一個材料性質連續的整體。因此在兩種材料的交界面上會產生應力的突變,在整個復合梁的橫截面上,應力不是連續的,因此可能出現兩個中性層。
七、思考題
1. 復合梁中性層為何偏移?
答:因為兩種材料的抗彎能力以及抗拉能力不同,導致在同等應力條件下,兩個截面對稱位置發生的應變不同。抗彎能力以及抗拉能力強的材料發生的變形小于另一種材料,因此中性層就向下偏移了。
2. 如何理解復合梁實驗中出現兩個中性層?
復合梁雖然中間是由物理或化學方法進行了連接,但是其實際上不是一個材料性質連續的整體。因此在兩種材料的交界面上會產生應力的突變,在整個復合梁的橫截面上,應力不是連續的,因此可能出現兩個中性層。
